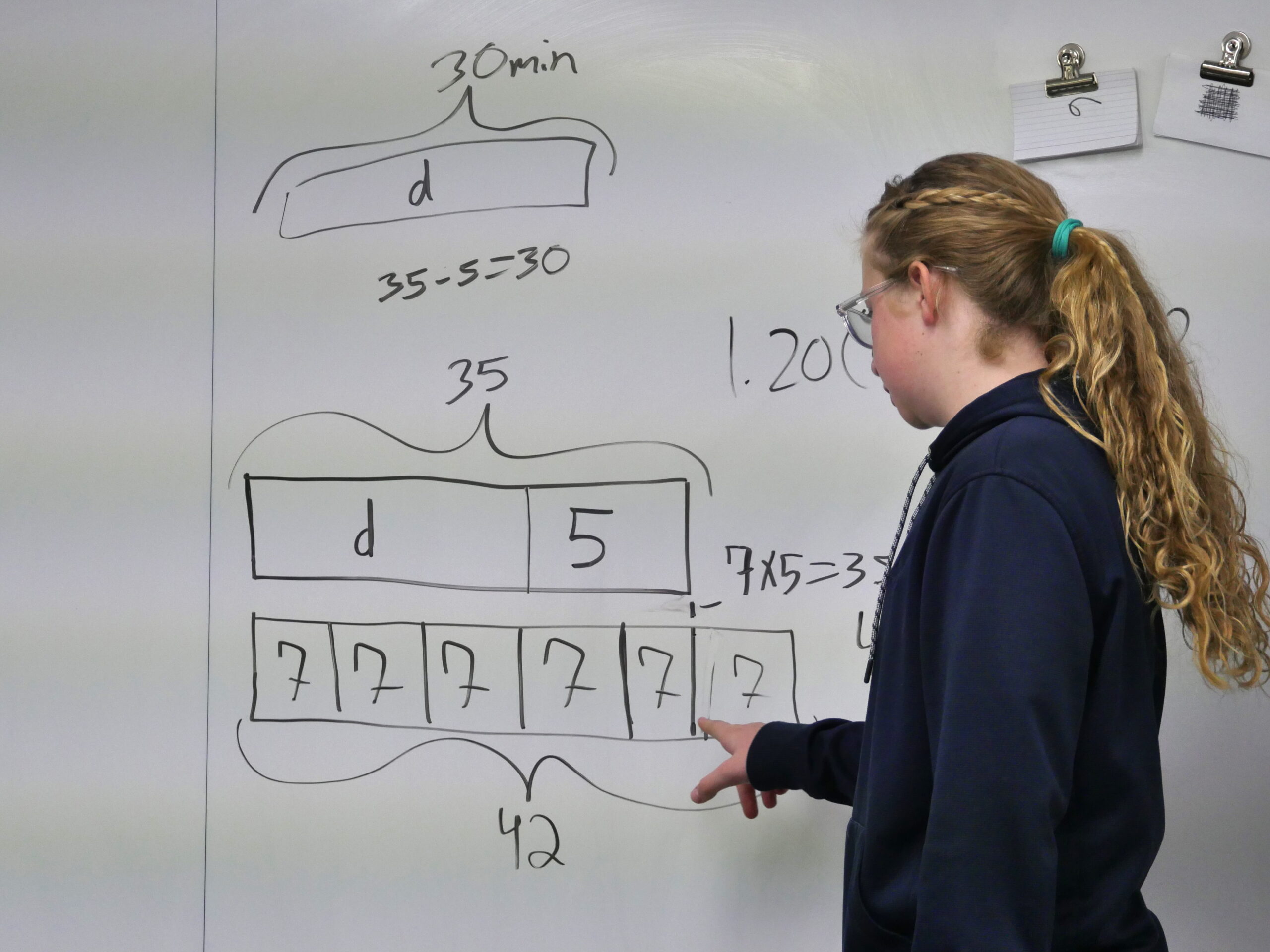“Is it diffusion?” “No, that’s in science! But it sounds like diffusion maybe…”
And, “You could count it? I don’t know, somehow count the difference between the two points?”
7th Grade Mathematicians are modeling and solving equations across both our 7 Standard and 7 Intensives classes. In 7 Intensive, students this week reasoned about equations in point-slope and slope-intercept form to match lines with their equations, and to simplify and compare equations that describe everyday situations, using both graphical and algebraic methods. In 7 Standard, students reasoned about diagrams that show changes through time and also wrote and evaluated equations in the form px + q=r and p(x+q)=r to describe everyday situations with unknowns.
In both classes, students used tools to make their reasoning visible, solved problems using more than one method, presented solutions to one another, and critiqued their own and others’ reasoning.
Their teachers guided their exploration, scaffolded their reasoning, and helped them notice more efficient or elegant methods. In 7 Standard, students were stretched to describe “distribution” in an equation, and what it represents, as well as to explain how an equation and a diagram represented the same situation. In 7 Intensive, students were challenged by graphing their own solutions to questions like, “what four lines connect these four points into a quadrilateral?” In each class, students also incorporated their own questions and interests—“Can you use theta in Desmos? I think I found a way to make a circle that connects all four points.”
I think I found a way to make a circle that connects all four points.
Whatever their current math pathway, our students practice process skills and build math understanding in community, living out our conviction that learning comes from both mistakes and curiosity, which everyone can practice.